[백준 10870 파이썬] - 피보나치 수 5

https://www.acmicpc.net/problem/10870

10870번: 피보나치 수 5

피보나치 수열 을 구해야 한다. 

n번째 피보나치 수를 f(n)라고 할 때 4번 째 피보나치 수 f(4)를 구하는 과정은 다음과 같다.

재귀적으로 각각의 결과값을 더한다. 

 

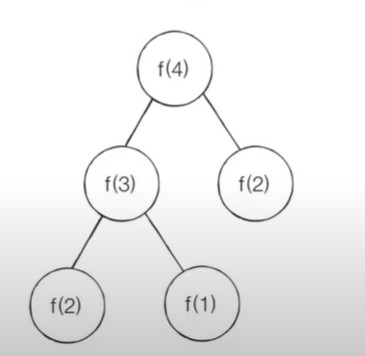
피보나치 수열 : 단순 재귀 소스코드

def fib(v):
  if v<=1: 
    return 1   
  return fib(v-1)+fib(v-2)

n=int(input())
print(fib(n))

 

아래 사진과 같이 단순 재귀 함수로 피보나치 수열을 해결하면 지수 시간 복잡도를 가지게 된다.

f(2)의 중복되는 문제 !!   비효율적인 시간복잡도 발생 '

 

 

백준 10870 문제는 n의 범위가  20보다 작다고 하니까 아직까지 시간 복잡도에 대한 에러는 없을 것이다.

 

만약 f(30)을 계산하기 위해 약 10억가량의 연산을 수행해야한다. 범위만 달라질 뿐인데 "시간초과"가 발생할 수 있다.

문제는 쉬운데 범위때문에 에러발생이 난다. 

 

피보나치 수열의 효율적인 해법 : 다이나믹 프로그래밍

  다이나믹 프로그래밍의 사용 조건을 만족하는지 확인한다

  1. 최적 부분구조 : 큰 문제를 작은 문제로 나눌 수 있다.

  2. 중복되는 부분 문제: 동일한 작은 문제를 반복적으로 해결한다.

 

 

구현하는 방법은 상향식, 하향식이 있다.

탑다운 ( 메모이제이션 : Memoization, Top-down)  :

한번 계산한 결과를 메모리 공간에 메모하는 기법 , 큰 문제를 해결하기 위해 작은 문제를 해결한다.

 

보텀업 (  Bottom-up)  :

작은문제를 해결해가면서 그 다음에 문제까지 차례대로 해결한다.

다이나믹 프로그래밍의 전형적인 형태는 보텀업 방식

결과 저장용 리스트는 DP 테이블이라고 부른다.

 

피보나치 수열 :탑다운 다이나믹 프로그래밍 소스코드

#한 번 계산된 결과를 메모이제이션 하기 위한 리스트 초기화
d=[0]*100

#피보나치 함수를 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
def fibo(x):
  #종료조건 (1 혹은 2일 때 1을 반환)
  if x==1 or x==2 :
    return 1
  #이미 계산한 적 있는 문제라면 그대로 반환
  if d[x]!=0:
    return d[x]
  #아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
  d[x]=fibo(x-1)+fibo(x-2)
  return d[x]

print(fibo(99))

피보나치 수열 :보텀업 다이나믹 프로그래밍 소스코드

#앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화

d=[0]*100

#첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1]=1
d[2]=1
n=int(input())

#피보나치 함수 반복문으로 구현 ( 보텀업 다이나믹 프로그래밍)
for i in range(3,n+1):
	d[i]=d[i-1]+d[i-2]
    
print(d[n])

이미 계산된 결과를 메모리에 저장하면 다음과 같이 색칠된 노드만 처리할 것을 기대할 수 있다.